Поляризация — одна из основных характеристик антенн. Для начала необходимо понять поляризацию плоских волн. Затем можно будет обсудить основные типы поляризации антенн.
линейная поляризация
Мы начнём понимать поляризацию плоской электромагнитной волны.
Плоская электромагнитная (ЭМ) волна обладает несколькими характеристиками. Во-первых, мощность распространяется в одном направлении (поле не изменяется в двух ортогональных направлениях). Во-вторых, электрическое поле и магнитное поле перпендикулярны друг другу и ортогональны друг другу. Электрическое и магнитное поля перпендикулярны направлению распространения плоской волны. В качестве примера рассмотрим одночастотное электрическое поле (поле E), заданное уравнением (1). Электромагнитное поле распространяется в направлении +z. Электрическое поле направлено в направлении +x. Магнитное поле направлено в направлении +y.
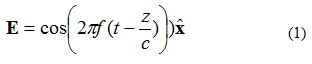
В уравнении (1) обратите внимание на обозначение: . Это единичный вектор (вектор длины ), который указывает, что точка электрического поля направлена вдоль оси x. Плоская волна показана на рисунке 1.
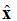
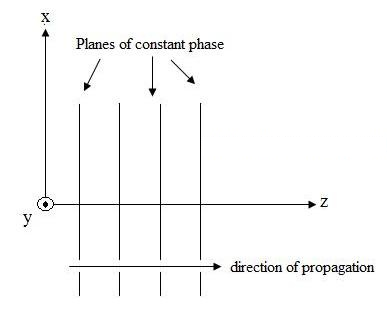
Рисунок 1. Графическое представление электрического поля, распространяющегося в направлении +z.
Поляризация — это траектория и форма распространения (контур) электрического поля. В качестве примера рассмотрим уравнение электрического поля плоской волны (1). Мы будем наблюдать положение, где электрическое поле (X,Y,Z) = (0,0,0) как функцию времени. Амплитуда этого поля показана на рисунке 2 в несколько моментов времени. Поле колеблется с частотой "F".
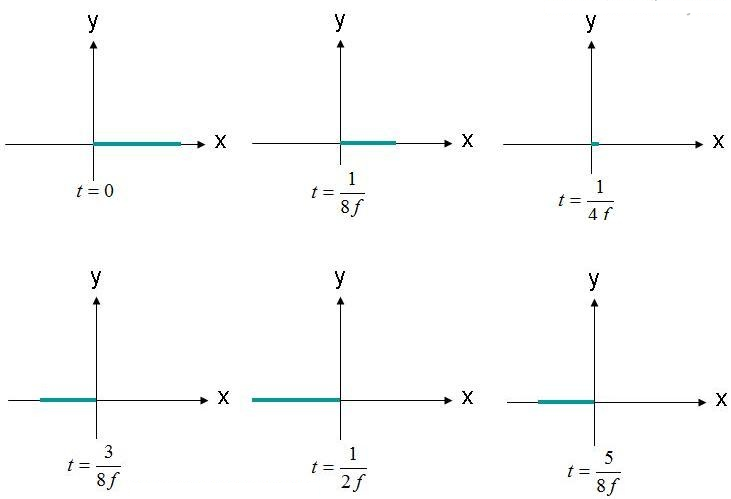
Рисунок 2. Наблюдайте электрическое поле (X, Y, Z) = (0,0,0) в разные моменты времени.
В начале координат наблюдается электрическое поле, амплитуда которого колеблется взад и вперед. Электрическое поле всегда направлено вдоль указанной оси x. Поскольку электрическое поле поддерживается вдоль одной прямой, можно сказать, что это поле линейно поляризовано. Кроме того, если ось x параллельна земле, это поле также описывается как горизонтально поляризованное. Если поле ориентировано вдоль оси y, можно сказать, что волна вертикально поляризована.
Линейно поляризованные волны не обязательно должны быть направлены вдоль горизонтальной или вертикальной оси. Например, волна электрического поля с ограничением, лежащим вдоль линии, как показано на рисунке 3, также будет линейно поляризованной.
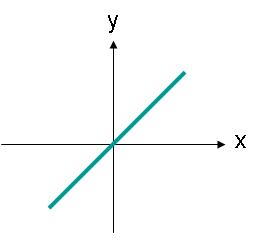
Изображение 3. Амплитуда электрического поля линейно поляризованной волны, траектория которой представляет собой угол.
Электрическое поле на рисунке 3 можно описать уравнением (2). Теперь есть x- и y-компоненты электрического поля. Обе компоненты равны по величине.
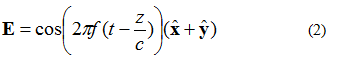
Следует отметить, что в уравнении (2) на втором этапе присутствуют xy-компонента и электронные поля. Это означает, что обе компоненты имеют одинаковую амплитуду в любой момент времени.
круговая поляризация
Теперь предположим, что электрическое поле плоской волны задается уравнением (3):
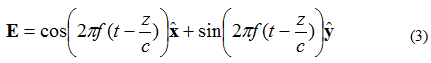
В этом случае элементы X и Y сдвинуты по фазе на 90 градусов. Если поле снова наблюдать как (X, Y, Z) = (0,0,0), как и раньше, то кривая зависимости электрического поля от времени будет выглядеть так, как показано на рисунке 4 ниже.
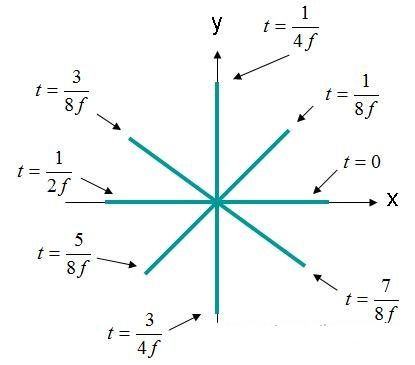
Рисунок 4. Напряженность электрического поля (X, Y, Z) = (0,0,0) область EQ. (3).
Электрическое поле на рисунке 4 вращается по кругу. Этот тип поля описывается как циркулярно поляризованная волна. Для круговой поляризации должны выполняться следующие критерии:
- Стандарт для круговой поляризации
- Электрическое поле должно иметь две ортогональные (перпендикулярные) компоненты.
- Ортогональные компоненты электрического поля должны иметь равные амплитуды.
- Квадратурные компоненты должны быть сдвинуты по фазе на 90 градусов.
При движении по экрану, изображенному на волновой диаграмме 4, поле вращается против часовой стрелки и имеет правостороннюю круговую поляризацию (RHCP). Если поле вращается по часовой стрелке, оно будет иметь левостороннюю круговую поляризацию (LHCP).
Эллиптическая поляризация
Если электрическое поле имеет две перпендикулярные компоненты, сдвинутые по фазе на 90 градусов, но равные по величине, то поле будет эллиптически поляризовано. Рассмотрим электрическое поле плоской волны, распространяющейся в направлении +z, описываемое уравнением (4):
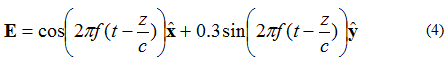
На рисунке 5 показано местоположение точки, в которой будет находиться конец вектора электрического поля.
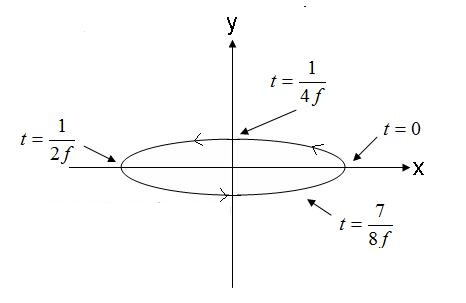
Рисунок 5. Электрическое поле мгновенной эллиптической поляризованной волны. (4).
На рисунке 5 поле, распространяющееся против часовой стрелки, будет иметь правостороннюю эллиптическую поляризацию, если оно распространяется за пределы экрана. Если вектор электрического поля вращается в противоположном направлении, поле будет иметь левостороннюю эллиптическую поляризацию.
Кроме того, эллиптическая поляризация определяется её эксцентриситетом. Это отношение эксцентриситета к амплитуде большой и малой осей. Например, эксцентриситет волны из уравнения (4) равен 1/0,3 = 3,33. Эллиптически поляризованные волны дополнительно описываются направлением большой оси. Волновое уравнение (4) имеет ось, в основном состоящую из оси x. Следует отметить, что большая ось может быть расположена под любым углом в плоскости. Угол не обязательно должен совпадать с осью X, Y или Z. Наконец, важно отметить, что как круговая, так и линейная поляризация являются частными случаями эллиптической поляризации. Эллиптически поляризованная волна с эксцентриситетом 1,0 является круговой поляризованной волной. Эллиптически поляризованные волны с бесконечным эксцентриситетом. Линейно поляризованные волны.
Поляризация антенны
Теперь, когда нам известно о поляризованных плоских электромагнитных полях, поляризация антенны определяется очень просто.
Поляризация антенны. Оценка поляризации антенны в дальней зоне — это поляризация результирующего излучаемого поля. Поэтому антенны часто обозначаются как «линейно поляризованные» или «правосторонние круговые поляризованные антенны».
Эта простая концепция важна для антенной связи. Во-первых, антенна с горизонтальной поляризацией не будет взаимодействовать с антенной с вертикальной поляризацией. В соответствии с теоремой взаимности, антенна передает и принимает сигнал совершенно одинаково. Следовательно, антенны с вертикальной поляризацией передают и принимают поля с вертикальной поляризацией. Поэтому, если вы попытаетесь передать сигнал с помощью антенны с вертикальной поляризацией и антенны с горизонтальной поляризацией, приема не будет.
В общем случае, для двух линейно поляризованных антенн, повернутых относительно друг друга на угол ( ), потери мощности из-за этого несоответствия поляризации будут описываться коэффициентом потерь поляризации (PLF):
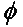
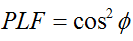
Следовательно, если две антенны имеют одинаковую поляризацию, угол между излучаемыми ими электронными полями равен нулю, и потери мощности из-за несоответствия поляризации отсутствуют. Если одна антенна имеет вертикальную поляризацию, а другая — горизонтальную, угол составляет 90 градусов, и передача мощности не происходит.
ПРИМЕЧАНИЕ: Изменение угла наклона телефона над головой объясняет, почему иногда можно улучшить качество приема. Антенны сотовых телефонов обычно имеют линейную поляризацию, поэтому вращение телефона часто позволяет выровнять поляризацию антенны, тем самым улучшая качество приема.
Круговая поляризация — желательная характеристика многих антенн. Обе антенны имеют круговую поляризацию и не страдают от потерь сигнала из-за несоответствия поляризации. Антенны, используемые в системах GPS, имеют правостороннюю круговую поляризацию.
Теперь предположим, что линейно поляризованная антенна принимает волны с круговой поляризацией. Иными словами, предположим, что антенна с круговой поляризацией пытается принимать волны с линейной поляризацией. Каков будет результирующий коэффициент потерь поляризации?
Напомним, что круговая поляризация представляет собой две ортогональные линейно поляризованные волны, сдвинутые по фазе на 90 градусов. Следовательно, линейно поляризованная (ЛП) антенна будет принимать только фазовую составляющую круговой поляризации (ЦП). Поэтому потери на поляризационное рассогласование в ЛП антенне составят 0,5 (-3 дБ). Это справедливо независимо от угла поворота ЛП антенны. Таким образом:
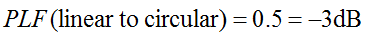
Коэффициент поляризационных потерь иногда называют поляризационной эффективностью, коэффициентом несогласования антенны или коэффициентом приема антенны. Все эти названия относятся к одному и тому же понятию.
Дата публикации: 22 декабря 2023 г.







